Facteur de puissance et tangente φ¶

Exemple introductif¶

Avant de réaliser un calcul d’écoulement de charge pour déterminer l’état électrique du réseau, il est bien sûr nécessaire de spécifier le comportement des charges ; or, dans un réseau alimenté en courant alternatif, indiquer uniquement la puissance consommée par une charge (grandeur généralement exprimée en kilowatts, appelée “puissance active” par les électriciens) est insuffisant pour caractériser précisément son comportement.

En effet, imaginons que l’on alimente, par une prise électrique standard, une “charge” constituée d’un simple condensateur ou d’une simple bobine. Cette “charge” ne consomme aucune puissance, puisqu’elle ne fait que se charger et se décharger alternativement à la fréquence du réseau, soit 50 Hz ; autrement dit, elle échange en permanence de l’énergie avec le réseau, mais comme elle restitue à chaque demi-période l’énergie reçue pendant la demi-période précédente, elle ne consomme aucune puissance. Un compteur électrique situé en amont de la prise indiquerait, à raison, une consommation nulle (0 kW), comme si aucune charge n’était alimentée par la prise. Cependant, un certain courant circule bien dans le réseau pour réaliser ces cycles de charge-décharge du condensateur ou de la bobine. Pour une même consommation de 0 kW, la situation est donc très différente selon que la prise alimente un condensateur ou une bobine, ou si elle n’alimente aucune charge : l’état électrique du réseau ne sera pas le même, car dans chaque cas, un courant différent circule dans le réseau. Cet exemple illustre l’affirmation précédente : le fait de spécifier la consommation de puissance d’une charge, en l’occurrence 0 kW, ne permet pas de caractériser avec suffisamment de précision le comportement d’une charge (sommes-nous dans le cas d’un condensateur, d’une bobine, ou d’une absence de charge ?), et donc ne permet pas de calculer l’état électrique du réseau.

Facteur de puissance et tangente φ¶

Pour caractériser entièrement une charge dans une étude d’écoulement de charge en courant alternatif, on doit en fait donner deux informations, et non pas une seule. Il existe différentes manières équivalentes de donner ces deux informations : on peut spécifier la puissance (active) et le facteur de puissance, ou encore la puissance (active) et la puissance réactive, ou encore la puissance (active) et la tangente $\varphi$ ou autrement encore… Toutes ces formulations reviennent au même.

Notion de facteur de puissance¶

La notion de facteur de puissance est usuellement utilisée pour décrire (partiellement) la consommation d’une charge.

L’idée essentielle est que l’on peut voir toute charge comme l’association d’une charge résistive et d’une charge de type “condensateur” ou au contraire de type bobine, ces deux comportements étant opposés l’un de l’autre[1]. Intuitivement, le facteur de puissance (noté “$\cos\left(\varphi\right)$”) mesure la pondération de chacun des deux types. Il s’agit d’une caractéristique de la charge qui varie entre 0 et 1, et qui peut être de type “inductif” ou “capacitif”.

Plus le facteur de puissance est proche de 1, plus la résistance sera “importante” par rapport à la bobine ou le condensateur. Par exemple, une charge avec un facteur de puissance égal à 0.9 inductif peut être vue comme l’association d’une résistance principale et d’une bobine relativement plus “petite” que la résistance. Une charge avec un facteur de puissance égal à 0.1 inductif peut être vue comme l’association d’une petite résistance et d’une bobine relativement plus “grosse” que la résistance. Les cas extrêmes sont les suivants :

Une charge avec un facteur de puissance égal à 1 est une charge purement résistive.
Une charge avec un facteur de puissance égal à “0, inductif” est une bobine.
Une charge avec un facteur de puissance égal à “0, capacitif” est un condensateur.

La figure ci-dessous permet de mieux se représenter les choses.

../../_images/Definition_Facteur_Puissance.png — Facteur de puissance pour une charge consommatrice¶

Notion de tangente φ¶

Si le facteur de puissance (ou “$\cos\left(\varphi\right)$”) est une caractéristique subie pour les charges (dépendante de leur nature plus ou moins résistive, inductive et capacitive) celui-ci peut être choisi pour la production. Dans ce cas, on préfère utiliser non pas la “$\cos\left(\varphi\right)$” mais la tangente $\varphi$, qui est définie comme étant le rapport entre la puissance réactive et la puissance active qui sont injectées par l’installation de production. Par exemple :

Une tangente $\varphi$ nulle signifie que l’installation de production injecte 100% de puissance active[2].
Une tangente $\varphi$ égale à 0.1 signifie que pour chaque Watt de puissance active injectée, l’installation de production injecte 0.1 VAr de puissance réactive.
Une tangente $\varphi$ égale à -0.4 signifie que pour chaque Watt de puissance active injectée, l’installation de production soutire 0.4VAr de puissance réactive.

Liens entre facteur de puissance, tangente φ, puissance active, puissance réactive et puissance apparente¶

Ces cinq grandeurs sont liées entre elles. On note $S$ est la puissance apparente, $P$ la puissance active, $Q$ la puissance réactive, $\cos\left(\varphi\right)$ le facteur de puissance et $\tan\left(\varphi\right)$ la tangente $\varphi$. Ces grandeurs et leurs liens sont représentés sur la figure ci-dessous.

Comme cela a déjà été évoqué, il suffit d’en spécifier deux pour caractériser le comportement d’une charge. Dans Grid Capacity, on demande à l’utilisateur de spécifier :

Pour une consommation : la puissance active et le facteur de puissance, ce qui permet d’en déduire la puissance réactive (notion utilisée par les électriciens pour quantifier le caractère plus ou moins inductif ou capacitif d’une charge, comme lorsque l’on utilise la notion de facteur de puissance).
Pour une production : la puissance active et la tangente $\varphi$, ce qui permet également d’en déduire la puissance réactive.

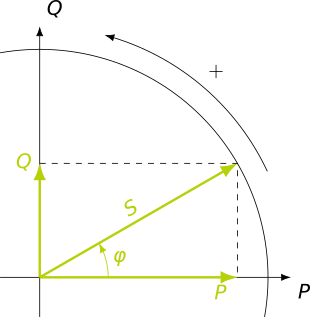
../../_images/Definition_Puissances.png — Définition des puissances actives, réactives, apparentes ainsi que de l’angle “$\varphi$”¶

La formule à utiliser pour calculer la puissance réactive, notée $Q$, à partir de la puissance active et du facteur de puissance est la suivante :

(1)¶\[\begin{split}Q=\left\{ \begin{aligned} \frac{P}{\cos\left(\varphi\right)}\cdot\sqrt{1-\cos^2\left(\varphi\right)} &\quad \text{si $P\neq0$ et $\cos\left(\varphi\right)\neq0$}\\ 0 & \quad \text{si $P=0$}\\ \text{invalide} & \quad \text{si $P\neq0$ et $\cos\left(\varphi\right)=0$} \end{aligned} \right.\end{split}\]

et pour calculer la puissance réactive à partir de la puissance active et de la tangente $\varphi$ : $$ Q=P\cdot\tan\left(\varphi\right). $$

Avertissement

Dans l’équation (1), on constate l’existence de cas particuliers :

si l’utilisateur fournit $P=0$ W, alors nous supposons que l’utilisateur souhaite une absence de charge ce qui conduit à $Q=0$ VAr également.
si l’utilisateur fournit $P\neq 0$ W mais $\cos\left(\varphi\right)=0$, alors il souhaite à la fois une charge consommant de la puissance active ($P\neq 0$ W) et à la fois une charge ne consommant exclusivement que de la puissance réactive ($\cos\left(\varphi\right)=0$). Cette demande étant incohérente, cela est interdit dans Grid Capacity.

Exemple

Une charge consommant 4 kW et 3 kVAr est caractérisée par une puissance apparente de 5 kVA :

\[ S^{\text{consommation}}=\sqrt{4~\text{kW}^2+{3~\text{kVAr}}^2}=5~\text{kVA}, \]

et un facteur de puissance de 0.8 :

\[ \cos\left(\varphi^{\text{consommation}}\right)=\frac{4~\text{kW}}{\sqrt{4~\text{kW}^2+{3~\text{kVAr}}^2}}=\frac{4}{5}=0.8. \]

Exemple

Un producteur injectant 9.8 kW et soutirant 2.0 kVAr est caractérisée par une puissance apparente de 10 kVA :

\[ S^{\text{production}}=\sqrt{9.8~\text{kW}^2+{\left(-2.0~\text{kVAr}\right)}^2}\approx 10~\text{kVA}, \]

un facteur de puissance de 0.98 :

\[ \cos\left(\varphi^{\text{production}}\right)=\frac{9.8~\text{kW}}{\sqrt{9.8~\text{kW}^2+{\left(-2.0~\text{kVAr} \right)}^2}}\approx 0.98, \]

et une tangente $\varphi$ de -0.20 :

\[ \tan\left(\varphi^{\text{production}}\right)=\frac{Q}{P}=\frac{-2.0~\text{kVAr}}{9.8~\text{kW}}\approx -0.20. \]

Valeurs typiques du facteur de puissance pour les charges¶

Une valeur de facteur de puissance typique pour les charges réelles, valeur couramment utilisée dans les études de réseau électrique, est “0.95, inductif”. Il s’agit donc d’une charge essentiellement résistive, c’est-à-dire qui consomme principalement de l’énergie électrique, mais qui dans une certaine mesure échange aussi de l’énergie avec le réseau, et ceci comme le ferait une bobine (et non pas comme le ferait un condensateur). Autrement dit, on peut distinguer deux transferts d’énergie : un transfert d’énergie principal, depuis le réseau vers la charge, et un transfert d’énergie secondaire qui consiste en des allers-retours permanents d’une petite quantité d’énergie entre le réseau et la charge, comme si notre charge était composée d’une “grosse” résistance (qui consomme de l’énergie) et d’une “petite” bobine (qui échange de l’énergie avec le réseau) côte-à-côte, en parallèle.

Astuce

Les valeurs courantes du facteur de puissance pour les charges sont comprises dans l’intervalle $[0.8;1]$, généralement avec un comportement inductif.

Dans Grid Capacity, la valeur par défaut du facteur de puissance pour les charges sera de 0.89, inductif.

En pratique, les charges électriques de nature essentiellement résistive sont par exemple celles qui contiennent des éléments de chauffage (chauffage électrique, grilles-pains, bouilloires…). Les charges de nature (résistive et) inductive sont les appareils qui contenant des bobinages, c’est-à-dire typiquement des transformateurs ou des moteurs électriques. Plus rarement, d’autres charges peuvent avoir un comportement de type (résistif et) capacitif.

Astuce

Les charges capacitives étant très rares par rapport aux charges inductives, le choix a été fait dans Grid Capacity de ne pouvoir définir que des facteurs de puissance inductifs pour les charges.

Valeurs typiques de tangente φ pour la production¶

Un producteur raccordé sur le réseau HTA n’injecte généralement que de la puissance active et a donc une tangente $\varphi$ égal à 0. Cependant, il peut être utile dans certains cas de choisir une autre valeur de tangente $\varphi$. C’est typiquement le cas lorsque le raccordement d’une installation de production entraîne le risque d’apparition d’une contrainte de tension haute sur un départ : dans ce cas, la solution de raccordement retenue peut consister à demander au producteur d’adopter un réglage de tangente $\varphi$ différent de 0 avec un comportement de type “inductif” (ou pour le formuler différemment, de “consommer une certaine quantité de puissance réactive”). En effet, de même qu’une injection de puissance active tend à relever la tension localement sur le réseau, une consommation de puissance réactive tend à la faire baisser localement. En jouant sur la tangente $\varphi$ de l’installation de production, on peut donc compenser partiellement ou totalement une élévation de tension causée par l’injection de puissance (active).

Différents types de réglages sont possibles : on peut par exemple programmer un onduleur photovoltaïque pour qu’il ait une tangente $\varphi$ constante, ou encore une tangente $\varphi$ variable en fonction de la tension. La solution la plus répandue actuellement consiste à choisir une tangente $\varphi$ constante, par exemple avec une valeur de $\tan\left(\varphi\right)=-0.4$ (valeur usuelle, répandue en pratique).

Si l’utilisateur de Grid Capacity est peu familier avec les notions présentées dans cette section, il est conseillé de conserver les valeurs par défaut du facteur de puissance et de tangente $\varphi$. Dans le cas contraire, il est possible de modifier les facteurs de puissance des consommateurs et les tangentes $\varphi$ des producteurs.

Effets sur le réseau d’une modification du facteur de puissance ou de la tangente φ¶

On a vu que le fait de modifier la tangente $\varphi$ (le facteur de puissance, respectivement) d’une installation de production (de consommation, respectivement), à puissance (active) produite (consommée respectivement) égale, revient à faire circuler dans le réseau le courant nécessaire à l’alimentation des cycles de charge-décharge d’une bobine ou d’un condensateur imaginaire situé(e) en parallèle de l’installation de production.

Ce phénomène provoque une variation de tension — ce qui est précisément le phénomène recherché lorsque l’on joue sur la tangente $\varphi$ pour faciliter le raccordement d’une installation de production — mais pas seulement. Le courant supplémentaire nécessaire à l’alimentation de la bobine ou du condensateur imaginaire vient s’ajouter ou se soustraire au courant qui circulait auparavant dans le conducteur, ce qui peut avoir pour effet de le faire baisser ou de le faire augmenter (les deux cas sont possibles). Cette variation du courant dans les conducteurs aura donc un effet positif ou négatif sur les pertes électriques par effet Joule, et sur le taux d’utilisation du conducteur (au sens où une augmentation du courant total réduit la marge disponible avant d’atteindre l’intensité maximale admissible par le conducteur du point de vue thermique, et inversement, une réduction du courant total augmente cette marge).

Synthèse sur les notions de facteur de puissance et de tangente φ¶

Les principaux points à retenir sur les notions de facteur de puissance et de tangente $\varphi$ sont les suivants.

Pour caractériser une charge en courant alternatif, indiquer uniquement la puissance (en kW) que cette charge consomme est insuffisant. Une deuxième information est nécessaire. Dans Grid Capacity, cette information est demandée à l’utilisateur sous la forme d’un nombre compris entre 0 et 1, appelé le facteur de puissance pour la consommation, et sous la forme d’un nombre appelé tangente $\varphi$ pour les producteurs.
Grid Capacity fournit par défaut des valeurs “raisonnables” du facteur de puissance et de la tangente $\varphi$. Ces valeurs peuvent être conservées par la grande majorité des utilisateurs.
La valeur du facteur de puissance est une caractéristique subie pour les charges, tandis que la tangente $\varphi$ peut être choisie (dans certaines limites) pour les installations de production.
Pour les consommateurs, les facteurs de puissance sont définis comme étant inductifs dans Grid Capacity. Ainsi, diminuer la valeur du $\cos\left(\varphi\right)$ fera baisser la tension et aura donc un effet positif (augmentation de la marge) vis-à-vis des contraintes de tension haute tandis que cela aura un effet négatif (une diminution de la marge) vis-à-vis des contraintes de tension basse.
Pour les producteurs, les tangentes $\varphi$ négatives correspondent à une consommation de réactif (comportement inductif) alors que les valeurs positives correspondent à une production de réactif (comportement capacitif). Ainsi, diminuer la valeur de tangente $\varphi$ (sous 0) fera baisser la tension et aura un effet positif (augmentation de la marge) vis-à-vis des contraintes de tension haute tandis que cela aura un effet négatif (une diminution de la marge) vis-à-vis des contraintes de tension basse. L’augmenter (au-dessus de 0) produira un effet inverse.
Hormis l’effet sur la tension, une modification du facteur de puissance ou de la tangente $\varphi$ aura également un impact sur les courants circulant dans les conducteurs, donc sur les pertes et sur les marges en courant[3]. Cet effet peut être positif ou négatif.
Une installation de production ne peut jouer sur sa tangente $\varphi$ que dans les limites de ses capacités constructives. Un onduleur de puissance supérieure aura des capacités constructives supérieures, mais aussi un coût supérieur.